 (1)
(1)© Vinokurov V.A. 2000
An experiment to check the formula for relativistic electron
trajectory radius in magnetic field of solenoid
V.A.Vinokurov
Abstract
An experiment with relativistic electron movement in solenoid static magnetic field is proposed. The experiment needs an electron source with energy from 300 keV to 2000 keV and magnetic field up to 1500 Gs. Independent measurement of three relativistic electron movement parameters are done in the experiment. These parameters are electron energy E, trajectory curvature radius R and magnetic field induction B. Experiment results is checking of functional dependence between E, R, B. The experiment motivations are 1) predictions of the condensation theory, 2) absence of direct experiments of such kind, 3) strange uncertainties in known experiments of similar kind.
PACS: 81.15.Fg
Keywords : Special relativity, magnetic field, curvature radius.
1. Experiment aims
Experiment aims are checking of the formula
 (1)
(1)
for a curvature radius R for plane movement of a relativistic electron with kinetic energy E and relativistic factor
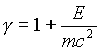 (2)
(2)
in homogeneous magnetic field of solenoid with induction B. Here m is electron rest mass, e is electron charge, c is light velocity. International system is used in formula (1).
2. Theoretical basis
Construction of continuous models for physical vacuum is popular modern area of studies. Many articles are now within soliton theory that treats particles as field condensations. I had offered the mathematical model for obtaining point particles far-action through continuous medium near-action ( see [1]).
The model starts from a stationary homogeneous isotropic medium that is described by an action integral of the form
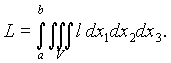 (3)
(3)
Here V is a space region, [a,b] is a time interval, l is a system Lagrangian. The action extremals are treated as physical states of medium. Particles in this theory are such medium states that displacements of medium points tend to zero at space infinity. Two asymptotic problems are solved in the theory. The first problem is determination of asymptotic structure of particle field at space infinity. The second problem is determination of asymptotic interaction of two particles when distance between its centers tends to infinity. It occurs that to solve these problems it is enough to know only quadratic part of the Lagrangian and a few first moments of current function of particles.
Constants in the quadratized Lagrange function are chosen so that its Euler equations are the Maxwell equations. So the Maxwell equations of electromagnetic field are obtained in the model. Following Poincare [2], the Lagrange function of particles is obtained by asymptotic evaluation of space integral in (3). That gives the Lagrange function for interacting particles system or for a particle in external field. In the case of a particle in external electrostatic field this procedure gives a classical relativistic Lagrange function. But in the case of a particle in external magnetostatic field of a solenoid the new model gives an improved Lagrange function that can essentially differ from classical relativistic Lagrange function for large velocities.
3. Electron interaction with solenoid
The new model gives new description for electron movement in magnetostatic field of a solenoid as in solenoid as out of it. The new model gives explanation of Aharonov-Bohm Effect, when an electron moves in space out of solenoid, in frames of classical Maxwell electrodynamics without quantum mechanics.
The main term of difference between improved Lagrange function and conventional one is value of order 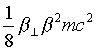 as
as ![]() . But main nonconstant part of Lagrange function is value of order
. But main nonconstant part of Lagrange function is value of order 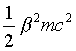 for that case. Here v is electron velocity,
for that case. Here v is electron velocity, ![]() is value of particle velocity that is orthogonal to solenoid axis,
is value of particle velocity that is orthogonal to solenoid axis, 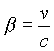 ,
, 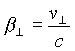 . So the difference is essential only when velocity
. So the difference is essential only when velocity ![]() is relativistic (
is relativistic (![]() is comparable with 1 ). The new Lagrange function for an electron in solenoid gives new more complicated trajectories those can be noncircular and unclosed. Functional relation between energy E, magnetic field induction B and trajectory curvature radius R changes for a case of plane circular movement of an electron around solenoid axis ( see [1] ). So independent measurement of three physical values E,B,R makes it possible to check the new theory.
is comparable with 1 ). The new Lagrange function for an electron in solenoid gives new more complicated trajectories those can be noncircular and unclosed. Functional relation between energy E, magnetic field induction B and trajectory curvature radius R changes for a case of plane circular movement of an electron around solenoid axis ( see [1] ). So independent measurement of three physical values E,B,R makes it possible to check the new theory.
But when checking the new theory, you should take in mind the following factors:
1) The model example is calculated only for a case of charged particle movement within an ideal solenoid.
2) The new theory is not local, i.e. only value of induction vector ![]() at the point
at the point ![]() , where an electron is, does not determine interaction as Aharonov-Bohm Effect shows.
, where an electron is, does not determine interaction as Aharonov-Bohm Effect shows.
3) Effective curvature radius R depends on relativistic factor γ by similar way for electron solenoid passing and by principally different way for stationary movement within solenoid ( see [1] ).
4) If ![]() is much less than 1 then trajectories do not differ essentially in the new model and the old one.
is much less than 1 then trajectories do not differ essentially in the new model and the old one.
4. Plan of the experiment
According to aforesaid I had proposed in the article [3] the following scheme of the crucial experiment with independent measurement of three parameters E,R,B of relativistic electron movement within solenoid. An electron moves in plane that is orthogonal to solenoid axis and includes the symmetry center of a finite solenoid. Cross section of the solenoid by this plane is shown in figure 1.
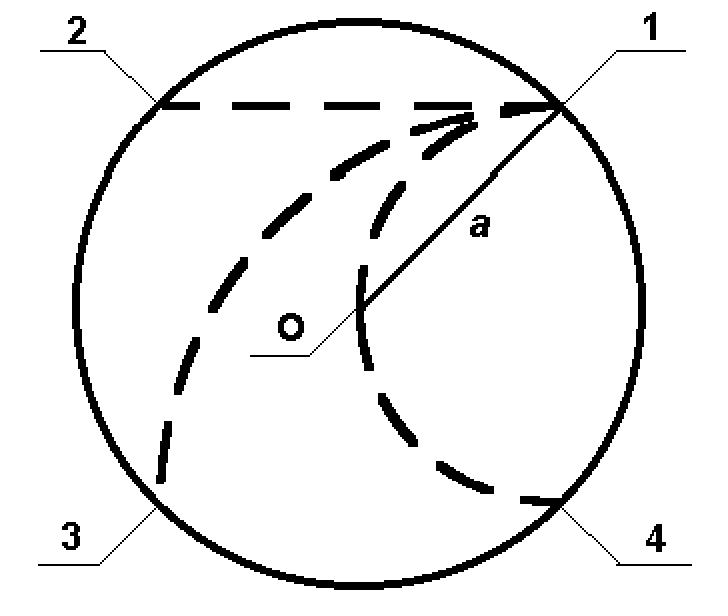
Figure 1. The first scheme of experiment.
An electron goes into solenoid at point 1. The angle between the electron velocity vector in point 1 and the radius from circle center O to point 1 is ![]() . A circle radius of solenoid interior cross section is a.
. A circle radius of solenoid interior cross section is a.
An electron goes out of solenoid in points 2,3,4 if induction B=0, ![]() ,
, ![]() accordingly. Dotted lines show electron trajectory in these three cases. Devices are set at points 2,3,4 to measure electron current value for given induction B. An electron comes into points 3 or 4 for conventional relativistic model when induction B is such, that
accordingly. Dotted lines show electron trajectory in these three cases. Devices are set at points 2,3,4 to measure electron current value for given induction B. An electron comes into points 3 or 4 for conventional relativistic model when induction B is such, that ![]() or
or 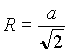 accordingly. An electron comes into points 3 or 4 for the new model when induction B has the other value as it is shown in tables 1 and 2. The tables are calculated for the case a = 5cm.
accordingly. An electron comes into points 3 or 4 for the new model when induction B has the other value as it is shown in tables 1 and 2. The tables are calculated for the case a = 5cm.
The following notions are used in tables 1-3:
E - electron (positron) energy in kiloelectronvoltes (keV);
![]() - magnetic field induction in Gauss (Gs), that is evaluated according to the classical relativistic theory;
- magnetic field induction in Gauss (Gs), that is evaluated according to the classical relativistic theory;
![]() - magnetic field induction in Gauss (Gs), that is evaluated according to the condensation theory.
- magnetic field induction in Gauss (Gs), that is evaluated according to the condensation theory.
Table 1 shows induction value ![]() of the old model and
of the old model and ![]() of the new model such that an electron goes out of solenoid at point 3.
of the new model such that an electron goes out of solenoid at point 3.
Table 1: Arc between input and output points is ![]() .
.
|
E |
γ |
|
|
|
|
|
|
50 |
1,098 |
102 |
109 |
7 |
7 |
6 |
|
100 |
1,196 |
139 |
158 |
19 |
14 |
12 |
|
150 |
1,294 |
164 |
198 |
34 |
21 |
17 |
|
200 |
1,391 |
183 |
233 |
50 |
27 |
21 |
|
250 |
1,489 |
199 |
265 |
66 |
33 |
25 |
|
300 |
1,587 |
212 |
297 |
85 |
40 |
29 |
|
700 |
2,370 |
277 |
518 |
241 |
87 |
46 |
|
1000 |
2,957 |
305 |
670 |
365 |
120 |
54 |
|
1500 |
3,935 |
337 |
917 |
580 |
172 |
63 |
Table 2 shows the same parameters for the case when an electron goes out of solenoid at point 4.
Table 2: The shortest arc between input and output points is ![]() .
.
|
E |
γ |
|
|
|
|
|
|
50 |
1,098 |
200 |
218 |
18 |
9 |
8 |
|
100 |
1,196 |
266 |
316 |
50 |
19 |
16 |
|
150 |
1,294 |
311 |
396 |
85 |
27 |
21 |
|
200 |
1,391 |
340 |
466 |
126 |
37 |
27 |
|
250 |
1,489 |
362 |
530 |
168 |
46 |
32 |
|
300 |
1,587 |
383 |
594 |
211 |
55 |
36 |
|
700 |
2,370 |
453 |
1036 |
583 |
129 |
56 |
|
1000 |
2,957 |
473 |
1340 |
867 |
183 |
65 |
|
1500 |
3,935 |
487 |
1834 |
1347 |
277 |
73 |
An electron source in the experiment can be an accelerator or radioactive material. If an accelerator is used as electron source then an electron beam must enter interior solenoid space through holes in solenoid coil and tube wall. If an electron source is radioactive material with conversion electrons then it is set in interior solenoid space with collimator to cut electrons with given velocity vector.
An electron beam can have essential divergence particularly in the case of conversion electron source. Detection at point 3 can give essential error in that case, but detection at point 4 have odds of semicircular method and reduces error produced by beam divergence at input point 1.
In force of that remark it can be proposed experiment modification for the case of conversion electron source with direct measurement of electron circular trajectory radius R by semicircular method. The experiment basis is fact, that as the old theory as the new one admit circular trajectories with center on solenoid axis in the plane, orthogonal to induction vector but in this case
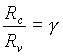
where ![]() and
and ![]() are values of radius in conventional theory and new one accordingly,
are values of radius in conventional theory and new one accordingly,
Scheme of this experiment is shown in figure 2.
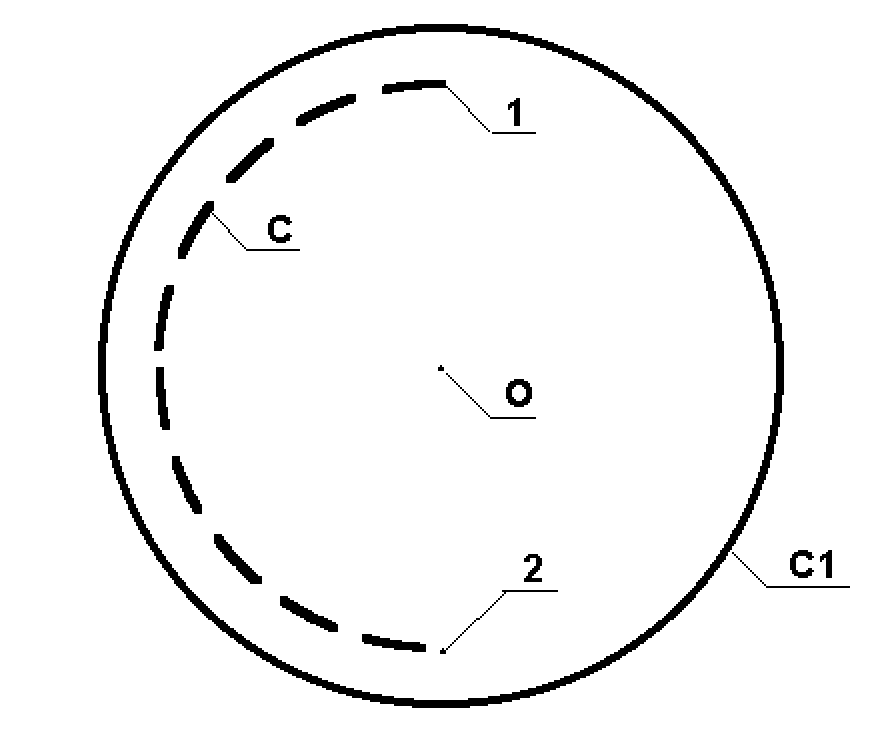
Figure 2: The second scheme of experiment.
Here exterior circle C1 is cross section of the inner wall of a solenoid tube, 1 is a conversion electron source, 2 is an electron detector. Dotted semicircle C is an electron trajectory. Point O is a mutual center of circle C1 and semicircle C. Table 3 shows induction values ![]() and
and ![]() such that an electron with energy E goes along trajectory C in the old theory and the new one accordingly. Those are conversion lines of bismuth isotope
such that an electron with energy E goes along trajectory C in the old theory and the new one accordingly. Those are conversion lines of bismuth isotope ![]() , and energy 976 keV relates to positron conversion.
, and energy 976 keV relates to positron conversion.
Table 3: Circular movement. R=5 cm.
|
γ |
|
|
|
|
|
|
|
481,7 |
1,904 |
290 |
552 |
262 |
90 |
48 |
|
975,6 |
2,910 |
320 |
932 |
612 |
191 |
66 |
Tables 1-3 shows that proposed experiment can be done at modern physical laboratory without extraordinary requirements to accuracy of implementation.
Detailed description of the experiment with conversion electron source is in article "Vinokurov V.A. A calculated scheme of the experiment to determinate trajectory parameters of relativistic electron in homogeneous magnetic field of solenoid (Russian)".
5. The experiment prehistory
After calculation of new trajectories of relativistic electrons in my model I had begun a search for already implemented experiments with conditions those meet my model requirements. I looked for experiments with relativistic electron movement in static magnetic field of solenoid and with independent measurement of three physical values: E,R,B. To my surprise, I did not find such experiments in the literature. Moreover, I had found strange uncertainties in some known experiments ( see [4-12] ) of such kind.
The article [4] by K.Irwin, W.W.Destler et al. describes an experiment of 1990 year with relativistic electron beam movement along a screw line in magnetic field of solenoid. Energy of an electron was E=560 keV. Magnetic field induction was B=370 Gs. Ratio 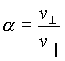 was declared as
was declared as
Electron beam moved along screw line in solenoid magnetic field in device, described in [5]. Experiment parameters are E= 580 keV, B= 6420 Gs,
α = 0.7. Discrepancy between designed value α = 0.35 and experimental value α = 0.7 was obtained in the experiment. Design of parameter α was made according to classical relativistic equations for electron movement in magnetic field. No discrepancy explanation in the article.V.S.Sarantzev and his group in Joint Institute for Nuclear Research (JINR) developed experiments with relativistic electron beam circular movement in magnetic field for collective acceleration of heavy ions (see [6] ). Assumed electron energy was 2-3 MeV . Trajectory radius was 35-40 cm. But the group did not measure electron energy by method that would be independent from classical relativistic formula (1). V.P.Sarantzev informed me about this fact during my visit to his laboratory in JINR in 1991.
A classic experiment to check Minkovski equations for electron movement in static electric and magnetic field is the experiment of W.Kaufmann [7]. This experiment is cited as basic experiment for special relativity theory in physical textbooks till today (see, for example, [8]). A.Einstein describes and analyses the Kaufmann experiment in work [9].
A piece of radium was used as a source of electrons in the experiment. Electrons were deflected by static electric and magnetic fields which were parallel to each other and orthogonal to electron velocity vector. Photographic plate was set in plane orthogonal to initial electron velocity vector. The plate fixed form of curve line that electron with different energies gave.
A.Einstein had stated that Kaufmann experiment data contradicted to his theoretical evaluations (see [9]). Experiment of such kind had been implemented by different authors till 1933 (see [8]). W.Pauli (see [10], � 29) declared that accuracy of the Kaufmann experiment was doubtful.
The following characters of the Kaufmann experiment do not let us use it for condensation theory checking:
1.Electron energy was unknown.
2.It was a situation with electron passing through area with magnetic field but not a situation with electron stationary movement within magnetic field.
3.Magnetic field in the experiment was a field of constant magnet but not a field of solenoid.
A famous classical work of β-spectroscopy foundations is K.Siegbahn article [11]. This article describes devices and experiments to determin
e electron energy by means of measurement of moving electron deflection in homogeneous magnetic field.The basic formula for the first Siegbahn method, "semicircular method", is relativistic formula (1) for radius R as function of relativistic factor
γ and induction B. It is naturally to suppose, from conventional metrology point of view, that the author had used independent measurement of E,B,R when β-spectrometer was calibrated. To my surprise, I had found that Siegbahn quite did not measure induction B to calculate unknown energy E from known B and R . He declared on page 29: "In order to determine the energy of the β-lines one must measure both H and ρ. Of these measurement that of H is the more awkward to perform and that which presents the greater possibilities of error. ... The results obtained by the different methods, however, show considerable discrepancies among themselves, which lie far beyond the limits of error estimated during the determinations." ( H is magnetic field intensity, ρ= R in our notations.) So he refused from absolute measurement of magnetic field intensity in semicircular method. And we can see that this basic work of β-spectroscopy has a strange methodological flaw that makes it unusable to check of formula (1) for radius.A research group of The Lebedev Physics Institute of The Russian Academy of Science under Dr.P.S.Strelkov leadership had executed an experiment, described here in point 4, in 1992 to my suggestion. But the group had met technical and methodical difficulties when experiment running and had failed to get necessary accuracy of measurement (research report [12]).
Conclusion. This point discussion shows that direct experiments with independent measurement of three parameters E,B,R for relativistic electron movement in solenoid magnetic field are not. Similar experiments [4,5,6,7,11,12], considered here, contain strange uncertainties. A direct precise experiment, described in point 4, is actual and feasible.
Remark 1. The sense of the experiment is independent measurement of energy E , induction B and radius R without using of formulas (1,2) for radius R as function of E and B. So electron energy must be measured by electrostatic method or by semiconductor detector.
6. Scientific value of the experiment
The experiment gives important information about equations that control relativistic particle movement in magnetic field. Positive result of the experiment will endorse the condensations theory. This theory gives direct expressions for mass, energy, charge, spin and other characteristics of a particle through its field structure. The condensation theory creates direct deductive scheme to develop all electromagnetic theory from the only action functional.
7. Technologic value of the experiment
Immediate consequence of positive experiment result is opportunity to build new charged particle high-energy accelerators those are thousand times less in size and costs then existing ones. That can principally expend area of accelerators technological applications in science, electronic, telecommunications.
The positive experiment result gives new impulse to solve a controlled thermonuclear fusion problem because the condensation theory furnishes the new more precise equations for movement of a charged particle in electromagnetic field and asserts that mathematical model, using for plasma description now, are essentially inexact, specially for long time of confinement and high energy particles.
References
[1] V.A.Vinokurov, Account of The Condensation Theory (Souz, Moscow, 1994).
[2] H.Poincare, Rend. Pal. V.21.(1906). p.129-176.
![]()
[4] K.Irwin, W.W.Destler, W.Lawson, J.Rodgers, E.P.Scannell, and S.T.Spang, J. Appl. Phys. B 69(2) (1991). p.627-631.
[5] J.L.Rullier, S.Alberti, B.G.Danly, E.Giguet, G.Gilotta, T.Kimura, W.L.Menninger, and R.J.Temkin, Nuclear Instr. and Method. Section A. 341(1994). p.93-97.

[7] W.Kaufmann, Ann. Phis. B 19 (1906). p.487.
[8] M.-A.Tonnelat, Les Principles de la Theorie Electromagnetique et de la Relativite (Paris, 1959).
[9] A.Einstein, Jahrb. d. Radioaktivitat u. Elektronik. B 4 (1907). p.411-462.
[10] W.Pauli, Theory of Relativity (Pergamon Press, 1958).
[11] K.Siegbahn, Arkiv for Matematik. Astronomi och Fysik. B 30A (1944) N.20. p.1-82.
