© Винокуров В.А.

Эксперимент по определению параметров траектории релятивистского электрона в однородном магнитном поле соленоида

В.А.Винокуров

 

Аннотация

Предлагается эксперимент по изучению движения релятивистского электрона в магнитном поле соленоида. Для проведения эксперимента требуется пучёк электронов с энергией от 300 до 2000 кэВ и постоянное магнитное поле с индукцией до 1500 Гс. Независимо измеряются три параметра, определяющие движение электрона: энергия электрона E, радиус кривизны траектории R и индукция магнитного поля B. Результат эксперимента — проверка вида функциональной зависимости между E,R,B. Необходимость проведения эксперимента мотивируется: 1) предсказаниями теории конденсации, 2) отсутствием прямых экспериментов такого рода, 3) странными неточностями в известных экспериментах такого рода.

 

 

1. Теоретическая и экспериментальная обоснованность эксперимента

В настоящее время одним из важнейших направлений фундаментальных научных исследований является изучение свойств физического вакуума, как путём конструирования его теоретических моделей на базе континуальных представлений, так и путём проведения ядерно-физических экспериментов. В работе [ 1 ] В.А.Винокуровым предложена, в частности, математическая модель для описания электродинамических процессов на базе лагранжевого подхода, восходящего к А.Пуанкаре [ 2 ], для получения динамики заряженных частиц из динамики электромагнитного поля. Одним из рассчитанных теоретических следствий новой теории, названной автором "теорией конденсации", является уточнение вида функции Лагранжа релятивистской заряженной частицы в магнитном поле соленоида. На базе уточнённого вида функции Лагранжа рассчитаны новые физические эффекты, имеющие важнейшие приложения в ускорительной технике, разработке мощных излучателей электромагнитных волн, управляемом термоядерном синтезе, производстве интегральных схем, телекоммуникациях.

Простейшим следствием теории конденсации является изменение связи между тремя параметрами, описывающими движение заряженной частицы в поле соленоида в классическом релятивистском случае: 1) кинетической энергией частицы E, 2) радиусом кривизны траектории R, 3) индукцией магнитного поля B. Для проверки предсказаний новой теории, таким образом, требуется независимое измерение указанных трёх параметров с достаточно высокой точностью. При проведенном анализе существующей научной литературы по экспериментам в релятивистской области с энергией электронов более 300 кэВ не обнаружено экспериментов с независимым измерением трёх параметров E, R,B с необходимым уровнем точности. Так в известном опыте Кауфмана [3] по проверке закона движения релятивистского электрона в постоянных электрическом и магнитном полях не была известна энергия электронов, магнитное поле не было полем соленоида и обнаруживались расхождения с предсказаниями специальной теории относительности [4].

В опытах К.Зигбана [5] по обоснованию полукругового метода бета-спектроскопии не измерялись энергия электронов и напряжённость магнитного поля, магнитное поле не было полем соленоида и неточно определялась энергия конверсионных электронов. В опытах В.П.Саранцева [6] с пучками релятивистских электронов в магнитном поле не измерялась независимо энергия электронов. В опытах К.Ирвина, У.У.Дестлера и др. [7] наблюдались расхождения результатов эксперимента с расчётами по классической релятивистской теории, но источники расхождений не были установлены. Аналогичные расхождения теории и эксперимента при движении релятивистских электронов в магнитном поле наблюдались в работе [8], причём причины расхождений также не установлены.

Таким образом, современное состояние теории и эксперимента делает актуальным проведение экспериментов по независимому измерению параметров E,R,B движения релятивистского электрона в поле соленоида. Актуальность эксперимента следует и из предсказываемых технологических и экономических следствий теории конденсации, оцениваемых в миллиарды долларов.

 

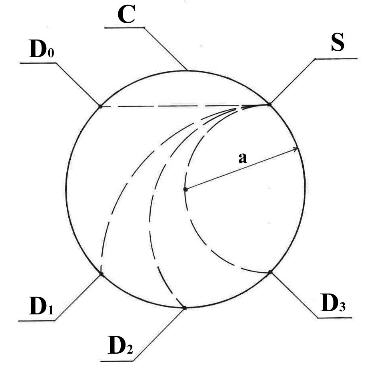
2. Предлагаемая схема эксперимента представлена на рисунке 1.

 

 

Рисунок 1. Схема эксперимента.

Пучок позитронов внутренней конверсии из источника S движется в однородном магнитном поле индукции B, создаваемом обмотками соленоида, и регистрируется полупроводниковыми диффузионно-дрейфовыми детекторами Источник и детекторы расположены на одной окружности радиуса a в плоскости, перпендикулярной оси соленоида, центр которой лежит на оси соленоида в его среднем сечении. Вся система помещена в вакуумную камеру, находящуюся внутри соленоида. При отсутствии магнитного поля позитроны попадают на детектор , служащий для контроля интенсивности источника. Изучается зависимость интенсивностей, измеряемых детекторами, от величины индукции магнитного поля.

Таблицы 1 и 2 рассчитаны для угла ввода пучка в , и радиуса — a=5см . Обозначения: E — энергия позитрона в килоэлектронвольтах, γ — релятивистский фактор позитрона, — требуемая индукция магнитного поля по классической релятивистской теории в гауссах, — требуемая индукция магнитного поля по теории конденсации в гауссах.

Таблица 1. Показания датчика . (Дуга между точками ввода и вывода - 180°.)

E g Bv Bc Bc-Bv
Bc-Bv
Bv
 ·100%


Bc-Bv
Bc
 ·100%

50 1,098 102 109 7 7 6
100 1,196 139 158 19 14 12
150 1,294 164 198 34 21 17
200 1,391 183 233 50 27 21
250 1,489 199 265 66 33 25
300 1,587 212 297 85 40 29
700 2,370 277 518 241 87 46
1000 2,957 305 670 365 120 54
1500 3,935 337 917 580 172 63

Таблица 2. Показания датчика . (Кратчайшая дуга между точками ввода и вывода - 90°.)

E g Bv Bc Bc-Bv
Bc-Bv
Bv
 ·100%


Bc-Bv
Bc
 ·100%

50 1,098 200 218 18 9 8
100 1,196 266 316 50 19 16
150 1,294 311 396 85 27 21
200 1,391 340 466 126 37 27
250 1,489 362 530 168 46 32
300 1,587 383 594 211 55 36
700 2,370 453 1036 583 129 56
1000 2,957 473 1340 867 183 65
1500 3,935 487 1834 1347 277 73

 

 

 3. Источник (рисунок 2)

Рисунок 2. Схема источника.

 

представляет собой тонкий слой вещества, содержащего изотоп , расположенного на дне тефлонового стакана с внутренним диаметром d и высотой L. Интенсивность источника N — полное число позитронов, испускаемы в единицу времени с единицы площади источника. При этом максимальный угол отклонения θ вектора скорости от оси стакана будет равен в отсутствии магнитного поля.

 

4. Детектор представляет собой цилиндрический полупроводниковый диффузионно-дрейфовый датчик диаметром 15 мм, помещённый в защитный стакан со входной поверхностью, ориентированной перпендикулярно пучку позитронов. Каждый детектор обслуживается своим спектрометрическим каналом. Чувствительная поверхность детектора — круг диаметром 12 мм, энергетическое разрешение — на уровне 0,1 % в диапазоне от 500 до 1000 кэВ. Максимальная скорость счёта — порядка 1000 (1/с).

 

5. Оценка интенсивности пучка

Источник с предполагаемой интенсивностью 100000 (1/()) будет давать на выходе из стакана ( см. рис. 2)

импульсов в секунду. Учитывая зависимость 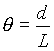, следующую из геометрии источника, получаем

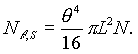
Поскольку в магнитном поле траектории позитронов искривляются, то для выхода позитронов из стакана требуется выполнение условия

где R — радиус орбиты позитрона.

Выбирая d = 1 мм, L = 10 мм, получаем θ = 0,1 , что соответствует . В этом случае согласно (1) . Требования ограничения (2) принимают вид 10 < 60 при R =7,5 см, а при R =3,75 см — вид 10 < 30 , т.е. выполняются.

При подходе к детектору пучок имеет радиус конуса расхождения

При R =7,5 см получаем 7,5 мм. Учитывая, что радиус чувствительной области детектора , получаем интенсивность, регистрируемую детектором

В нашем случае для детектора , подставляя в (4) = 7,5 мм, 6 мм, получаем Что является достаточной интенсивностью для выполнения планируемых измерений.

 

6. Предполагаемые результаты

При двух значениях энергии позитрона E=481,665 кэВ и E=975,615 кэВ предполагается измерение углового положения φ точки пересечения траектории позитрона с базовой окружностью, на которой расположены источник и детекторы, и величины соответствующей индукции магнитного поля B. Независимое измерение трёх параметров: 1) энергии позитрона E, 2) угла φ, 3) индукции B — позволит проверить выполнение формулы для ларморовского радиуса орбиты релятивистского позитрона в системе СИ:

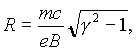
где v — скорость позитрона, m — его масса покоя, e — заряд, c — скорость света, — релятивистский фактор.

Основной источник погрешностей связан с расходимостью пучка и при θ = 0,1 даёт 6 % ошибки в определении угловой величины. Для повышения точности возможно: 1) увеличить интенсивность источника, 2) уменьшить расходимость пучка, 3) проводить измерения по центру тяжести кривой зависимости интенсивности счёта детектора от индукции магнитного поля. Следует заметить, что при измерении детектором радиуса окружности позитрона влияние угла расходимости θ уменьшается до относительной ошибки величины , что приводит к точности 1–2 %.

Список литературы

[1] Винокуров В.А. Очерк теории конденсации. — М.: Союз, 1993.

[2] Poincare H. Sur la dynamique de l'electron. — Rend. Pal. 1906. v.21. p.129–176.

[3] Kaufmann W. Ann. Phis. 1906. 19. p.487.

[4] Einstein A. Uber das Relativitatsprinzip und die aus demselben gezogenen Folgerungen. Jahrb. d. Radioaktivitat u. Eletronik. 1907. 4. 411–462. (Русский перевод статьи в книге "А.Эйнштейн. Собрание научных трудов. т.1. — М.: Наука, 1965", с. 65 – 114.)

[5] Siegbahn K. Studies in Beta-Spectroscopy. Arkiv for Matematik. Astronomi och Fysik. 1944. Bund 30A. N.20. p.1–82.

[6] Саранцев В.П. и др. Первый этап наладки прототипа коллективного ускорителя тяжёлых ионов. Часть 1. Сообщения ОИЯИ. Дубна. 1976. Р-9-10053.

[7] Irwin K., Destler W.W., Lawson W., Rodgers J., Scannell E.P. and Spang S.T. Second generation, high-power, fundamental mode large-orbit gyrotron experiments. J. Appl. Phys. 69(2). 1991. p.627–631.

[8] Ruller et al. High-power CARM and harmonic gyro-amplifier experiments. Nuclear Instr. and Method. Section A. 341(1994). p.93–97.



ГЛАВНАЯ СТРАНИЦА
Hosted by uCoz